earth from the outside in

1. From zero to monsoon

Hi everyone! In my intro post, I said I wanted to publish a miniature version of pan-gaia online, with only one dimension. But what does that mean? What does a “miniature version” entail? Where is this doggone dimension pointing??

This post begins a series explaining the ideas behind pan-gaia. We will start from zero - with nothing defined - and, gradually, develop a planetary model that can produce large-scale features of our real Earth’s climate, like ice caps, ocean currents, and monsoons (thus the name). I will tend to prefer covering scientific concepts over implementation details. At the end of the series, hopefully I’ll have a model that can be implemented and put up on itch.io.

In this post, I’ll start by laying out what we’re trying to do, and why it’s so interesting. Then, in the second half, I’ll briefly describe a 0-dimensional energy balance model. This model is very simple and very well-studied, and we’ll build off of it in the next post.

2. What do we want?

We’d like to make predictions about the climate of a rocky planet, that is, by some criteria, Earth-like.

We might want these predictions to learn about the Earth; or understand how climates of rocky planets work in general; or even predict if an exoplanet might be hospitable to us. Or maybe we just want a cool setting for a tabletop campaign.

As for focusing solely on rocky, Earth-like planets, I’m just establishing this as a ground rule for the series. Here are three justifications:

1. There’s more data to work with. We know a lot more about the Earth than we do about Jupiter or Saturn, even though their atmospheres are larger and far more dramatic than Earth’s.
2. It’s probably more interesting. A vaguely Earth-like planet might have life on its surface. Gas giants probably don’t! ¹
3. Given that we want to model at least Earth-like planets, from the above two points, it’s easier to focus only on them. Other planets operate in different physical regimes that would have to be modelled separately. Venus’s atmosphere is mostly supercritical CO2. The gas giants don’t have well-defined surfaces. And so on.

What is a climate?

“But it’s a fool’s errand”, I hear you grumble. “You can’t predict the weather: it’s chaotic”. Indeed it is! We are talking about two separate things here, weather and climate.

The distinction between climate and weather is not exact, but, broadly, weather means the actual physical conditions, at a certain time and place. Weather means it’s raining today, snowing tomorrow, a hurricane is coming in. Weather is (as the NOAA puts it) what you experience when you step outside on any given day.

Climate, on the other hand, is an average condition. Climate means it’s mild here in the winter, rainy most of the year, that you feel icy-cold when you swim in the sea. The climate is less chaotic than the weather, because it reduces all those daily variations to general probabilities.

Even so, by definition, climate is dependent on weather to to some extent. In particular, it depends on weather patterns that happen often, and across a wide area.

• If a river swells suddenly and floods once, but never again, the flooding is not described by the climate.
• If the river is constantly flooded, it’s still not necessarily part of the climate. Maybe there’s a gigantic log raft stopping it up.
• If most rivers in the area flood almost every March, there is probably some broad, stable cause, like a monsoon, or spring snowmelt, that emerges again and again from the chaos of the weather. Now it’s part of the climate.

If we widen our scope, the climate can also describe more fundamental things that we take for granted, out of the whole realm of physically allowed conditions. I will quote from the first chapter of Raymond Pierrehumbert’s Principles of Planetary Climate, because he’s so darn eloquent about this:

In the summer, ice cream will melt when left out in the sun, but steel cooking pots don’t. Trees and grass do not spontaneously burst into flame every afternoon, and a glass of water left outdoors in the summer does not boil. Away from the tropical regions, it often gets cold enough for water to freeze in the wintertime, but hardly ever cold enough for alcohol to freeze.

Why? Why is anything the way it is on Earth at all? That’s also something we want to answer.

Everything is connected

All these facts and conditions and large-scale patterns are connected together because, ultimately, they are all jammed up against each other, sharing the same media: the air, sea, land, ice, etc. They are part of a whole Earth system. (Get ready to read that phrase a lot.) All the components influence each other, and are influenced by each other.

And they aren’t totally static! The climate changes as the Earth system changes, slowly, over decades. Further, many climate features oscillate between predictable values, on regular or irregular cycles. Some of these oscillations are easy to explain: the middle latitudes get more sunlight in summer than in winter, and so, they oscillate between warmer and colder every year. Other oscillations can be much longer, dozens of millennia long. For instance, ice ages seem to happen on a schedule, once every 41,000 years. But, before some transition in the past, they happened once every 100,000 years. It’s an open question as to why.

Other oscillations are driven by parts of the Earth system pushing and pulling on each other dynamically, with some delay, like there’s an invisible spring connecting them. In the Pacific, two important examples are the El Niño–Southern Oscillation and the Madden-Julian Oscillation. Both of these cycles are like vast machines, coupling the air and sea together in immense conveyor belts of heat and moisture, and forming teleconnections between places that don’t even adjoin each other. It’s dizzying to think that, when the Java Sea gets a little cold, it pushes on the stratosphere in a gigantic, airy arc, leading to a dry winter in Alberta. But this specific interaction actually happens quite often.

We have just started to peer into the many ways in which everything in the Earth system connects to everything else.

How should we approach it?

Whew! Evidently, making these predictions is a Big Question. And, often, scientists resort to the Big Question Models to find answers. The biggest of these are called General Circulation Models (GCMs), and they’re the programs that run on supercomputers at places like ECMWF and NCAR. ^{2 3} These programs split up the Earth system into thousands of little boxes in 3 dimensions, and simulate them over time (which could count as a fourth dimension).

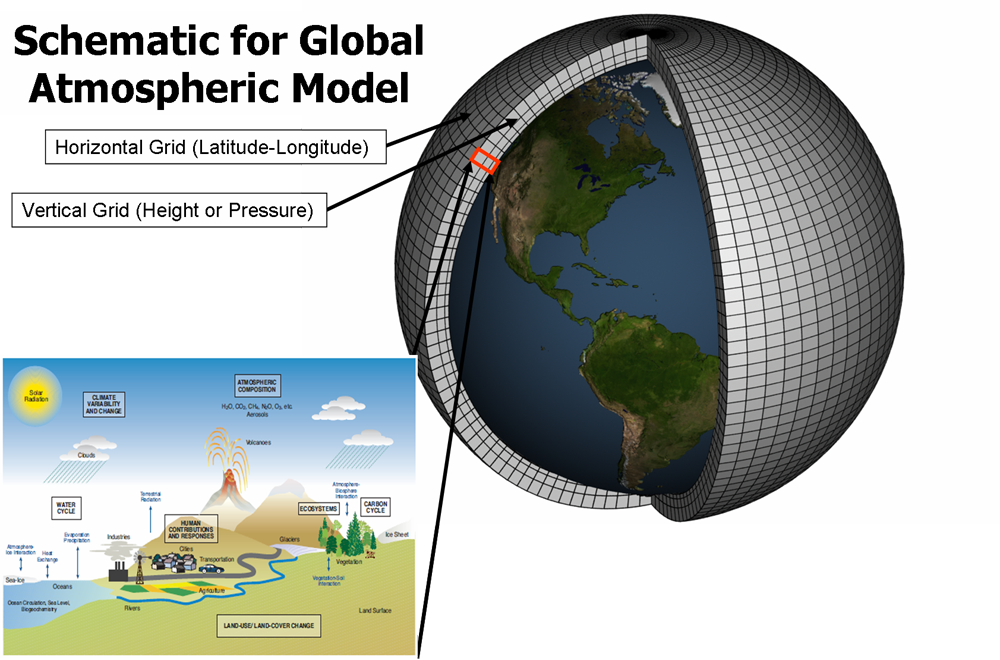
If this is the competition, you can start to feel a little overwhelmed. How the heck are we supposed to implement this ourselves? I guess we’ll need to draw a grid on the Earth, or something. Oh, but what type of grid? Do we have to include all the features from the start, since I said everything was connected? Also, does anyone here know FORTRAN 90? Or have a supercomputer…?

3. Our first model

Actually, none of that is necessary! Not yet. We can get a long way towards understanding the climate without needing a computer at all, through careful analysis, a calculator, and maybe a pen and paper.

This is a good thing! Climate simulation is a tricky business, so as our planetary model gets more complicated, it’s nice to know we’ll have simpler models against which we can compare our complicated models’ results.

In fact, we’re going to start our planetary model without splitting up the Earth at all. We’re going to zoom waaaay out, and start by looking at the planet as a single entity, a little mote of dust suspended in a sunbeam. We will try to balance the energy entering and exiting this entity. Compared with the 3-dimensional GCMs and their many fiddly little boxes, this model will have no variation across the planet whatsoever, just a single datum, a point. So, we can call it a 0-dimensional model.

Warning: this means math is coming, but very mild math, promise.

Starting from the outside

Imagine that you’re standing on the moon and looking at the Earth.

(RIP to William Anders, who took this photo from Apollo 8 in 1968, and died recently.)

The outer boundary of the Earth system is not hard and fixed. The upper atmosphere just trails off, getting thinner and thinner, until it blends smoothly into outer space. Still, as you peer at it from a distance, the border between Earth and space looks pretty sharp to you.

If you had a magic wand, you could pick some height way above Earth’s surface - 100 or 150 kilometers up ⁴, so high that all of the atmosphere is obviously below it - and inscribe a shimmering, intangible sphere around the planet.

Think about this spherical boundary we’ve just inscribed. What’s inside it, and outside it? What crosses this boundary?

1. All of the matter of the Earth system is inside this sphere. Outside the sphere, there’s almost no matter for millions of kilometers around, except for the Moon, a few asteroids, and some interplanetary dust.
2. With the exception of the solar wind, some meteors, and the occasional spacecraft, virtually zero matter crosses the spherical boundary.
3. Some electromagnetic energy crosses the boundary inward. Almost all of it is coming in a single parallel beam, from the Sun. Moonlight comes a faint second, followed by energy from all other sources in the Universe, including distant starlight. Let’s call this incoming stream shortwave radiation (SW), because it’s mostly in shorter wavelengths emitted by the sun: UV, visible, and some near-infrared rays.
4. Conversely, energy exits the boundary outward from Earth. Most of it is either heat being radiated by the planet, or shortwave energy (e.g. light) that’s bounced off of it. Let’s call the former type longwave radiation (LW), because it’s almost all in the infrared.

The upshot is that, 99.9% of the time, nothing but energy is crossing the boundary. That’s the only way Earth interacts with the rest of existence. If a cheeky alien built a really, really high-resolution television screen all around the spherical boundary, that could video-capture all the radiation coming in one side and re-emit it out the other side, you wouldn’t be able to tell. (Until you tried to come home.)

Let’s make two simplifying assumptions. First, we will assume that exactly zero matter crosses the spherical boundary. Second, the only incoming energy will be from the Sun, ignoring moonlight and starlight. Finally, we’re going to give the spherical boundary a nice name: the Top of Atmosphere (TOA). If you think about the reason we conjured the boundary into being, the top of Earth’s atmosphere is the smallest radius it can possibly be.

Incredible! Believe it or not, we now have all the information we need to draw a physical diagram of the entire visible universe under these assumptions. Behold:

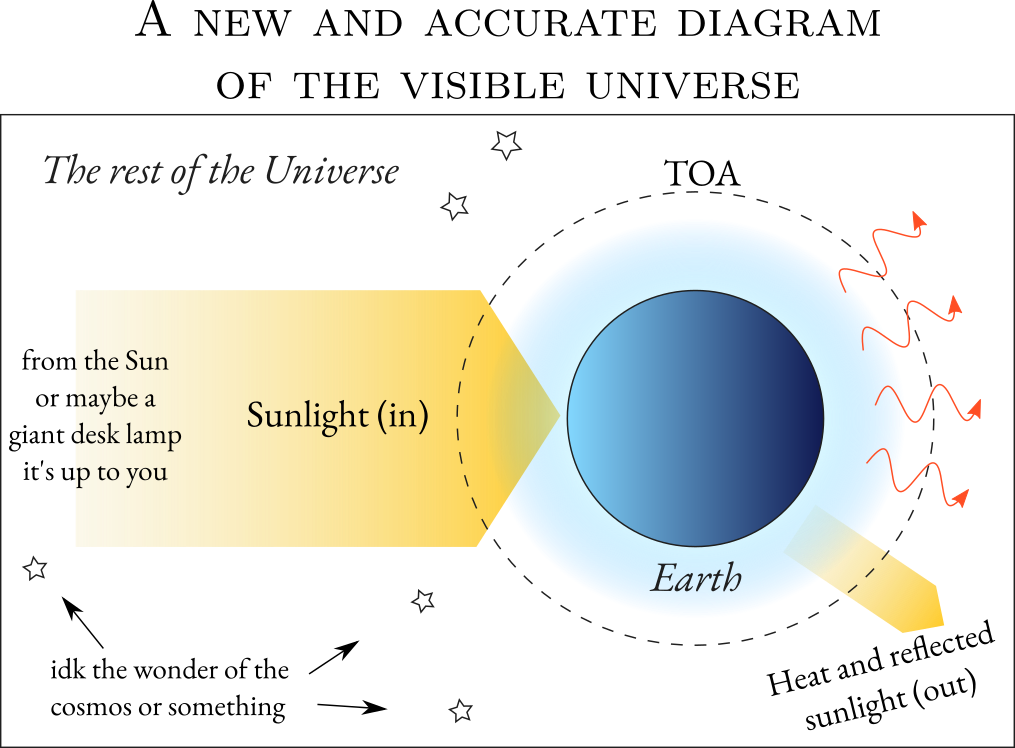
The universe outside is big and uninteresting to us. All we care is that, across the TOA, energy is flowing in and out at some rate. The energy coming in is shortwave, and the energy going out is a mix of shortwave and longwave. When it leaves, it goes off into space, never to be seen again.

Energy inside the TOA has to be conserved, like everywhere else in the universe. So, if these two flows are unequal, the net effect will be a gain or loss in energy, applied to the matter in the interior (i.e. the Earth system). This should continue until something happens (without specifying how), and the flows are in equilibrium again - that is, balanced. Then (here comes the math!):

$$ \mathrm{SW\ in} = \mathrm{SW\ out} + \mathrm{LW\ out} $$

Energy balances

This is the basis for our first planetary model, an energy balance model. As we mentioned, it’s 0-dimensional: we’re ignoring all variations in space and time, and focussing on a planet-wide equilibrium. Much better writers than me have covered this topic, in particular Brian Rose at the University of Albany, and (once again!) Raymond Pierrehumbert, so please forgive me if my treatment of the subject is a little cursory.

Coming in

First off, we’re going to prescribe our major input, the incoming shortwave radiation. This means we just pull a starting value out of a hat. At such a vast distance from the Sun, the shortwave radiation forms a perfectly parallel beam of constant intensity. Every object of any size at this distance, whether the Earth, the Moon, or an astronaut, is getting lit up with the same amount of sunlight per unit area, or flux density, which is measured in Watts per square metre.

The name for flux density from the Sun is the solar constant, denoted $S_0$. Currently, for our Sun, its value is:

$$ S_0 = 1362\ \mathrm{W/m}^2 $$

Whoa, OK! I said I wouldn’t start chopping up the Earth, much less into metre-square bits. But it’s nice to work with “normalised” values like this, where they’re always measured per-metre-squared. This way, it doesn’t matter how big a planet (or area of a planet) is, as long as the same phenomena are happening at every point.

From the Sun’s point of view, the round planet looks like a flat circle, with the same radius as the planet. So, a disk-shaped beam ends up hitting the planet. However, whatever the planet’s radius is, its (spherical) area is exactly 4 times the area of the beam:

So, normalised to the area of the planet, the shortwave radiation hitting it is exactly one-quarter of the solar constant. ⁵

$$ SW_{in} = S_0 / 4 = 340.5\ \mathrm{W/m}^2 $$

Bouncing off

Now, as we mentioned, part of the shortwave radiation bounces off into space. If you can see something from orbit, actually, you’re getting hit by reflected shortwave radiation. (Unless it’s an artificial light.) Just look at all the shortwave radiation flying off into space behind these astronauts:

How much bounces off is an extremely involved question. In the limit, you have to consider everything on the Earth under daylight, how reflective it is, multiple bounces and reflections, etc… but again, we only care about a whole-planet average value. Luckily for us, scientists have worked out just that, using satellite measurements. It’s called the Bond albedo, denoted $\alpha$: $$ \alpha_{\mathrm{Earth}} \approx 0.3 $$ An albedo of 0 would mean no light was reflected. An albedo of 1 would mean it was all reflected. (Clean snow has an albedo very close to 1.) Earth therefore reflects about 30% of the SW radiation that hits it.

This is another prescribed value for our model. If it kind of strikes you as cheating, well, good! That’s the investigative spirit. Later, we’ll be able to try replacing it with a predicted value from some kind of model we develop, one which explains the Bond albedo as a result of physical phenomena, instead of just trusting a number off the internet. But using a reasonable prescribed value gives us some idea of what results to expect from later, more complex models.

Anyway, albedo is just a dimensionless fraction of the incoming radiation across all wavelengths: $$ SW_{\mathrm{reflected}} = \alpha \cdot SW_{in} = 102.1\ \mathrm{W/m}^2 $$ So what remains, and gets absorbed by the Earth, is: $$ SW_{\mathrm{absorbed}} = (1 - \alpha) \cdot SW_{in} = 238.4\ \mathrm{W/m}^2 $$ This last figure is also called Absorbed Solar Radiation (ASR).

Radiating away

Only one piece of the model remains! Recall that the Earth is in equilibrium when incoming and outgoing energy are balanced across the TOA. We’ve dealt with incoming shortwave radiation, and reflected shortwave radiation, so our partial model is now:

$$ \underbrace{(1 - \alpha) \cdot \frac{S_0}{4}}_{(\mathrm{SW\ in} - \mathrm{SW\ out})\ =\ \mathrm{ASR}} = \mathrm{LW\ out} $$

To fill in a value for $\mathrm{LW\ out}$, let’s think about what it is. Every object made of matter emits thermal radiation. The total power of this radiation is proportional to the object’s effective temperature to the fourth power, and is given by the by the Stefan-Boltzmann law:

$$ \mathrm{SW\ out} = \epsilon \sigma T_{\mathrm{eff}}^4 $$

Four things to note:

1. This is the energy flux across the whole EM spectrum ⁶, and is again in $W / m^2$. An object with a larger surface area emits more total energy (not flux) than a smaller one.
2. We say effective temperature, $T_{\mathrm{eff}}$, to remind ourselves that it’s not the actual temperature throughout the planet, but the temperature exposed by the surface. ⁷
3. $\sigma$ is the Stefan-Boltzmann constant, $\approx 5.67 \times 10^{−8}\ W/m^2\cdot K^4$.
4. $\epsilon$ is the emissivity of the object; it lies between 0 and 1. An emissivity of 1 is only a theoretical upper limit achieved by perfect black bodies. Every other object can be said to emit a fraction of what its black-body radiation would be.

By the way, this is a partial answer to what process balances the incoming and outgoing radiation (remember that we didn’t want to assume how). Hotter objects radiate more heat; in fact, the radiated heat grows with the fourth power of temperature. If there’s too much energy coming in, the planet heats up until it’s emitting enough thermal radiation to reach equilibrium. Conversely, when the incoming energy is too weak, the planet cools down.

I say partial because, in reality, the albedo also changes with temperature, in some pretty non-linear and wacky ways. Water’s albedo, for instance, changes pretty drastically when it freezes. We’ll cover that in the next post.

It should be noted that most of the time emissivity refers to a specific property of a material, like water or dirt. But here, we’re pretending the Earth is a single object whose external properties match those of the real Earth. So $\epsilon$ is an effective emissivity, as if the pretend Earth was made entirely of some uniform material.

What is the Earth’s effective emissivity? Instead of prescribing you another value, we’re going to stop here and use our model to figure it out. Exciting!

Putting it all together

Gaze upon the might of this model.

$$ \underbrace{(1 - \alpha) \cdot \frac{S_0}{4}}_{\mathrm{ASR}} = \underbrace{\epsilon \sigma T_\mathrm{eff}^4}_{\mathrm{OLR}} $$

When the planet is in equilibrium, the net absorbed SW radiation (which we called ASR) equals the outgoing LW radiation (which we can shorten to OLR).

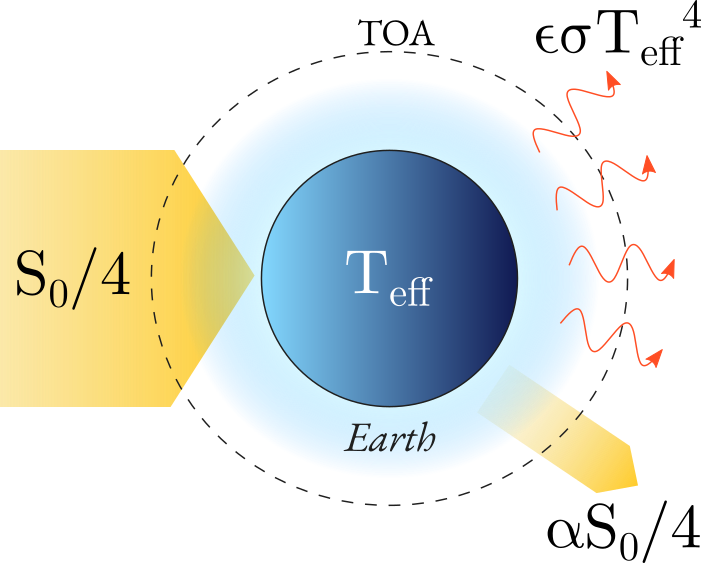
Our model has three free parameters:

1. $S_0$, the solar constant, which is not really related to the planet; it’s purely a property of (a) the Sun, and (b) how far we are from the Sun.
2. $\alpha$, the Bond albedo, which measures how much radiation (from 0% to 100%) reflects off the planet.
3. $\epsilon$, the effective emissivity, which measures how efficiently (from 0% to 100%) the planet emits its heat as thermal radiaiton. This is what we are trying to figure out.

And the only state variable is $T_\mathrm{eff}$, the effective temperature of the planet. If we do some algebra to rearrange the model, we can solve for $T_\mathrm{eff}$:

$$ T_\mathrm{eff} = \sqrt[4]{\frac{(1 - \alpha) S_0}{4 \epsilon \sigma}} $$

Using the model to discover something

Let’s start throwing some numbers into it. First, what would $T_\mathrm{eff}$ be if the Earth had 0 albedo and unity emissivity, like a perfect blackbody?

$$ T_\mathrm{eff} = \sqrt[4]{\frac{(1 - 0) \cdot 1362\ \mathrm{W/m}^2}{4 \cdot 1 \cdot \sigma}} = 278.4\ \mathrm{K} $$

So it would be about 5 degrees Celsius.

What if we now give the planet its real Bond albedo, but keep the emissivity at 1? This isn’t such a bad choice, on the face of it. Ice and water, for instance, have emissivities of about 0.99 and 0.96, respectively… and the Earth is mostly water.

$$ T_\mathrm{eff} = \sqrt[4]{\frac{(1 - \mathbf{0.3}) \cdot 1362\ \mathrm{W/m}^2}{4 \cdot 1 \cdot \sigma}} = 254.6\ \mathrm{K} $$

Yow! The 30% reduction in ASR was enough to plummet the temperature to 18.6 degrees Celsius below zero. Even with a 30-degree variation between the poles and the Equator (remembering that $T_\mathrm{eff}$ is an average), this would still render the tropics somewhere near or below freezing. What’s going on?

We’ve been given pretty reliable values for $S_0$ and $\alpha$. The only remaining free parameter is $\epsilon$. So the effective emissivity must not be 1, and, in particular, because of the way emissivity is defined, it must be less than 1.

If the surface of the Earth really does have an emissivity close to 1 (like water or ice), then something is going on between the surface and the TOA to trap some of its thermal radiation inside. Congratulations! By examining what the model predicted under certain conditions, we have discovered the greenhouse effect. ⁸

As it turns out, the current global-average surface temperature of Earth is about 15 degrees Celsius, or 288.2 Kelvin. Given this, we rearrange the model equation again, to solve for emissivity:

$$ \epsilon = (1-\alpha)\frac{S_0}{4} \cdot \frac{1}{\sigma T_\mathrm{eff}^4} $$ $$ = (1 - 0.3) \frac{1362\ \mathrm{W/m}^2}{4} \cdot \frac{1}{5.67 \times 10^{-8} \cdot (288.2\ \mathrm{K})^4} \approx 0.609 $$

So Earth has roughly the same emissivity as rusty iron.

Final remarks

The 0-dimensional energy balance model only contains three free parameters, and one of them only has to do with the Sun. Take a second to think about what the other two (albedo and emissivity) signify.

Everything that distinguishes Earth from any other arbitrary object, floating in space at the same distance from the Sun as we are, is caught up in those two numbers: every gust of air, every cloud, every ocean wave, every blade of grass, every person, every thing that lives. From the outside, standing on the moon, their only effects are to make Earth sort of reflective, and sort of inefficient at radiating heat. But in a very pretty way.

I am glad for any of you who have come to this blogpost before seeing an undergraduate-level climate science course, and thus got to experience the wonder of me restating what is basically a lecture note from the first week. Every lecture I’ve seen covering the 0-D energy balance model goes through the motions of deriving everything except the effective emissivity, before (in mock surprise) declaring “what’s this? It cannot be! The greenhouse effect!” But this basic plot (with newer and more exciting discoveries) will continue to come up, as we develop our model and gain predictions from it. That’s the whole fun of this business.

Stay tuned for the next post, where we will introduce our first dimension: time. Thanks for reading!